There are two main types of heaps:
  • Max-Heap: For any given node, its value is greater than or equal to the value of its children. This means the largest element is always at the root of the tree.
  • Min-Heap: For any given node, its value is less than or equal to the value of its children. The smallest element is always at the root.
A heap is not a sorted structure — it’s partially ordered to make insertion and removal of the min/max element efficient (typically O(log n) time). Heap Pn

​
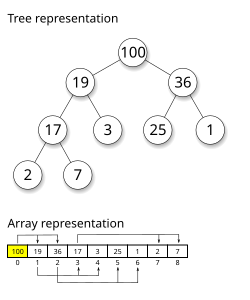
Analogy: Priority Queue

Priority Queues: This is the most common use case for heaps. A priority queue is an abstract data type where each element has a priority, and the element with the highest priority is served first. Heaps are the perfect underlying data structure for this, as they provide O(1) time complexity to find the highest (or lowest) priority element and O(log n) for insertions and deletions. Imagine a hospital emergency room where patients are treated based on severity:
  • The patient with the highest priority (most critical) is seen first
  • New patients are inserted in the queue, and the system ensures the most critical stays on top
That’s exactly how a priority queue, implemented using a heap, works. Heapsort Algorithm: Heaps are the foundation of the heapsort sorting algorithm. It works by first building a max-heap from an array, and then repeatedly extracting the maximum element and placing it at the end of the array. This results in an efficient sorting algorithm with a time complexity of O(n log n). https://en.wikipedia.org/wiki/Heap_(data_structure)